ストレイテナーと確率9(7の続き)
ストレイテナーと確率7では、
”「シャッフルで曲選択していって60分でリセット」を繰り返したら手持ちの曲全部聴き終わるまでにどんだけかかるんだ?”というのを検証した。
結果的にそのときは95回の「60分シャッフル」を繰り返すことで手持ち全曲を聴き終えたのだが、
確率の問題なので100回を超える時もあるし70回で終わるときもある。
ではその平均(最も頻度の高い回数)はどこなのか?というのは前回の終わりで疑問になっていた。
で、今回それを検証してみようと思い立ち、前回のプログラムを少し改造して実行してみた。
シミュレーション用のプログラムはほぼ前回の流用なので省略する。
簡単に言えば前回の(3)を何度も呼び出すようなループを上位に一つつけただけである。
前回は「60分シャッフルで聴き終わる」を1回やって終了するものだったが、
これを規定回数繰り返して結果の情報を大量に採取するように改造した。
この規定数はとりあえず10万回とした。
⇒当初100万にしていたのだが予想以上に時間がかかったので10万に変更した。
10万回でのシミュレーション実行時間は約6分程度であった。
ただ、確率により変動するため、これもあくまで一例である。(10分以上かかるときもあるだろう)
結果がこれ↓
| 終了までの回数 | その回で完了した試行合計数 |
|---|---|
| 53 | 2 |
| 54 | 1 |
| 55 | 3 |
| 56 | 10 |
| 57 | 11 |
| 58 | 18 |
| 59 | 37 |
| 60 | 55 |
| 61 | 87 |
| 62 | 116 |
| 63 | 141 |
| 64 | 181 |
| 65 | 224 |
| 66 | 284 |
| 67 | 376 |
| 68 | 505 |
| 69 | 588 |
| 70 | 675 |
| 71 | 791 |
| 72 | 914 |
| 73 | 1014 |
| 74 | 1137 |
| 75 | 1254 |
| 76 | 1369 |
| 77 | 1551 |
| 78 | 1629 |
| 79 | 1656 |
| 80 | 1826 |
| 81 | 1973 |
| 82 | 2040 |
| 83 | 2003 |
| 84 | 2124 |
| 85 | 2176 |
| 86 | 2290 |
| 87 | 2315 |
| 88 | 2304 |
| 89 | 2259 |
| 90 | 2255 |
| 91 | 2265 |
| 92 | 2244 |
| 93 | 2319 |
| 94 | 2217 |
| 95 | 2207 |
| 96 | 2107 |
| 97 | 2127 |
| 98 | 2121 |
| 99 | 1982 |
| 100 | 1976 |
| 101 | 1897 |
| 102 | 1754 |
| 103 | 1778 |
| 104 | 1635 |
| 105 | 1603 |
| 106 | 1581 |
| 107 | 1497 |
| 108 | 1508 |
| 109 | 1356 |
| 110 | 1359 |
| 111 | 1294 |
| 112 | 1221 |
| 113 | 1142 |
| 114 | 1093 |
| 115 | 1059 |
| 116 | 1079 |
| 117 | 946 |
| 118 | 855 |
| 119 | 911 |
| 120 | 796 |
| 121 | 701 |
| 122 | 722 |
| 123 | 688 |
| 124 | 661 |
| 125 | 606 |
| 126 | 599 |
| 127 | 565 |
| 128 | 532 |
| 129 | 513 |
| 130 | 491 |
| 131 | 462 |
| 132 | 445 |
| 133 | 391 |
| 134 | 358 |
| 135 | 374 |
| 136 | 341 |
| 137 | 331 |
| 138 | 296 |
| 139 | 302 |
| 140 | 256 |
| 141 | 239 |
| 142 | 266 |
| 143 | 217 |
| 144 | 226 |
| 145 | 188 |
| 146 | 166 |
| 147 | 190 |
| 148 | 147 |
| 149 | 145 |
| 150 | 144 |
| 151 | 132 |
| 152 | 143 |
| 153 | 108 |
| 154 | 120 |
| 155 | 103 |
| 156 | 102 |
| 157 | 106 |
| 158 | 83 |
| 159 | 95 |
| 160 | 65 |
| 161 | 93 |
| 162 | 73 |
| 163 | 69 |
| 164 | 56 |
| 165 | 45 |
| 166 | 71 |
| 167 | 51 |
| 168 | 52 |
| 169 | 46 |
| 170 | 45 |
| 171 | 40 |
| 172 | 36 |
| 173 | 42 |
| 174 | 36 |
| 175 | 41 |
| 176 | 22 |
| 177 | 20 |
| 178 | 19 |
| 179 | 20 |
| 180 | 27 |
| 181 | 20 |
| 182 | 21 |
| 183 | 17 |
| 184 | 20 |
| 185 | 13 |
| 186 | 20 |
| 187 | 18 |
| 188 | 17 |
| 189 | 17 |
| 190 | 10 |
| 191 | 12 |
| 192 | 9 |
| 193 | 10 |
| 194 | 6 |
| 195 | 15 |
| 196 | 7 |
| 197 | 8 |
| 198 | 5 |
| 199 | 8 |
| 200 | 7 |
| 201 | 6 |
| 202 | 5 |
| 203 | 5 |
| 204 | 4 |
| 205 | 3 |
| 206 | 3 |
| 207 | 4 |
| 208 | 4 |
| 209 | 2 |
| 210 | 2 |
| 211 | 4 |
| 212 | 4 |
| 213 | 6 |
| 214 | 5 |
| 215 | 1 |
| 216 | 2 |
| 217 | 2 |
| 219 | 3 |
| 220 | 3 |
| 221 | 3 |
| 223 | 1 |
| 226 | 1 |
| 227 | 3 |
| 230 | 1 |
| 231 | 3 |
| 232 | 2 |
| 233 | 2 |
| 237 | 1 |
| 238 | 1 |
| 239 | 1 |
| 252 | 1 |
| 255 | 2 |
| 257 | 1 |
| 267 | 1 |
| 271 | 1 |
| 276 | 1 |
「その回で完了した試行合計数」の総和を取ると上述した規定回数の10万になる。
赤太字にしてわかるようにしてあるが、
「その回で完了した試行合計数」の最大は2319回で、該当する最頻値は93回だった。
前回10回分の平均値をとって97.5という値を算出しているが、そこよりは少し低い値になっているものの、大体近い値だったという考察になりそうである。
前回の結果として載せてある「95回で聴き終る」というのもおおよそ平均に近い。
数値を見ればなんとなく想像がつくが、これをグラフにすると以下のようになる↓
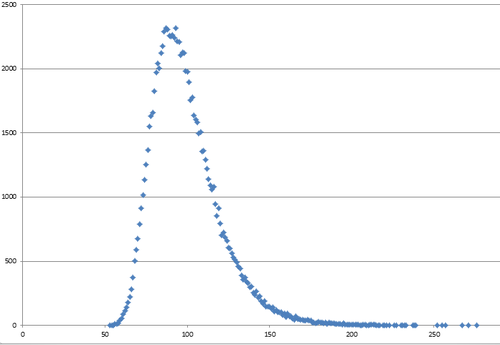
少し右側に伸びているが、いわゆる正規分布に近い形をしていることがわかる。
山なりになっている部分の山頂付近を示す値が上述した「93回で聴き終った」に該当する部分にあたる。
60分で聞ける曲数は大体14~15曲であることがストレイテナーと確率2からわかっているので、
(有り得ないはずだが)60分シャッフルの各回がそれぞれ重複することなくストレートに聴き終えた場合、
257/15=17.13333333…が大体の理論上の最低値になるわけか。
今回のシミュレーション結果では最小値は53回であるが、この値は53/17.1333…で、理論値のおおよそ3倍にあたる。
要するに、53回の60分シャッフル内での重複は1曲平均多くても3回程度だった、というように考察できるわけか…?
平均的に93回で聴き終るというのであれば60分シャッフル繰り返し内での重複回数は93/17.1333…で大体5.42…になるので、
1曲平均5回から6回は重複している計算になる。
そう考えると半分近い重複で済んでいる計算になるからやっぱりレアケースだったのだろう。
今回は60分シャッフルを10万回実行しているが、この回数を増やしていくと最終的には理論的な最小値の17.1333…あたりを記録するケースもあるのだろうが、
その場合はどれほどの回数の実行が必要なのか…気が遠くなる。
この「10万回」はintで指定しているが、intどころかlong型でも対応できないくらい天文学的に大きな数値を必要としそうだ。
(もちろん確率の問題だから10万どころか極論1でも”起こり得る”のは事実なのだが)
なお、今回のシミュレーションの最大値は276回となっているが、
上述したようにこの検証には理論的に最小値が決められている一方で、
運が悪いと何回やっても「前までに聴いた曲」になるから理屈でいえば最大値には歯止めがない(いくらでも大きくなり得る=∞になり得る)。
今回の検証は60分シャッフルを10万回繰り返したわけだが、
恐らくこの回数を100万、1000万…と増やしていくと、つられてこの「最大値」もどんどん大きくなるだろう。
今回のグラフの右側(最大値方面)が粘り強く広がっているのにはこうした事情もあるはずだ。
